Techculture: Cryptografie

Einer der ältesten Verschlüsselungen kommt von Caesar, dem römischen Diktator. Er verschlüsselte damals mit einer Chiffre seine Texte. Danach ging es weiter mit Vigenère Chiffre, die einen soliden Schutz aufwies, aber nicht richtig angewandt wurde. Dann kommt ein Zukunftssprung in die Gegenwart mit der Binärverschlüsselung. Heutzutage verwendet man RSA, RSA hat den Vorteil, dass ein öffentlicher und ein privater Schlüssel existiert und somit kein Geheimcode weitergegeben werden muss.

Caesar Chiffre

Es heißt Caesar, weil der Diktator im alten Rom, diese Verschlüsselungstechnik verwendet hat. An sich ist es einfach nur eine Verschiebung im Alphabet, sprich es wird der dritte Buchstabe, vom Ursprungsbuchstaben, verwendet. Wenn A = 1 ist, wäre A verschlüsselt 4 und somit D. Z ist 26 und wäre damit 3 somit C.

Beispiel

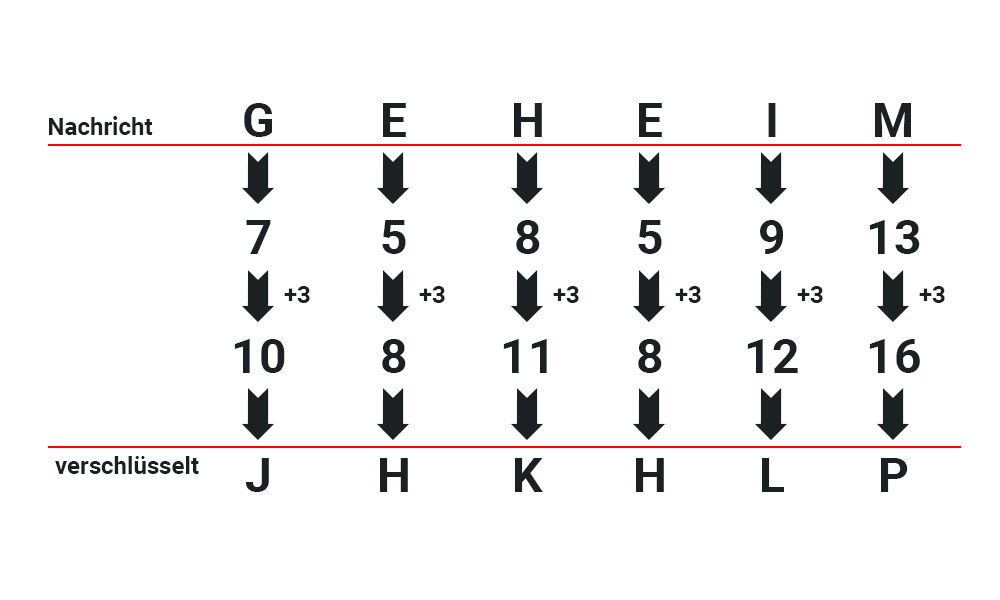
Sicherheit

Für damalige Verhältnisse was die Schiebechiffre sicher, aber in der Heutigen, ein leichtes für Codeknacker. Man muss einfach nur die durchschnittliche Häufigkeit von Buchstaben vergleichen und schon hat man die Chiffre.
Des weiteren kann solche Verschlüsselung mit 25 Versuchen entschlüsseln, da der jeweilige Buchstabe einfach nur ausgetauscht werden muss.

Vigenère Chiffre

Diese Verschlüsselung ist eine Weiterentwicklung, von der Caesar Chiffre. Diese wurde 1508 von dem deutschen Trithemius entwickelt und nach seinem Tot publik. Es wurde das Alphabet auf der X und Y Achse in eine Tabelle geschrieben und dann wurde der zu verschlüsselnde Text mit einem Geheimwort codiert.

[TABELLE]

In der Tabelle, war die erste Zeile das normale Alphabet von A bis Z. Die zweite Zeile fing mit B an und hörte mit A auf. Sprich jede Zeile war um 1 verschoben. Dadurch war die X Achse das Alphabet und die Y Achse das Alphabet. Dann hat man sein Text genommen und ein Geheimwort. Nehmen wir wieder das erste Beispiel und wollen das Wort GEHEIM verschlüsseln. Als Passwort nehmen wir TAUBEN, dann sucht man zuerst den ersten Buchstaben von GEHEIM, also das G, auf der X Achse und geht dann das erste Zeichen von TAUBEN, also T, auf der Y Achse und schaut sich den Wert von G-T an. Das wäre dann Z. Der komplette verschlüsselte Text wäre dann ZEBFMZ.

Bei einem privaten Treffen konnte man das Passwort weitergeben und in den Nachrichten dieses Passwort verwenden, damals galt diese Technik als unknackbar. Theoretisch wäre das Heutzutage auch noch der Fall, wenn man ein Text verwendet, der genau so lang ist wie der zu verschlüsselnde Text. Es wurde aber nur ein recht kurzes Passwort verwendet und dadurch kamen Doppler rein und dadurch konnte der Text entschlüsselt werden.

Binärverschlüsselung

Da die Binärverschlüsselung Ähnlichkeiten mit der Vigenère Chiffre hat, möchte ich diese zusammen behandeln. Bei der Binärverschlüsselung, werden die Buchstaben in Zahlenwerte umgewandelt, dies passiert mit der ASCII Tabelle. Das Wort GEHEIM wäre laut der ASCII Tabelle 71|69|72|69|73|77, dies ist eine international anerkannte Zeichentabelle um für den Computer Buchstaben in Zahlen umzuwandeln, da der Computer nichts mit Buchstaben anfangen kann, sondern nur mit Einsen und Nullen bzw. Strom kein Strom. Der Computer versteht aber auch keine, sagen wir, 6, da der Computer halt nur 1 für Strom und 0 für kein Strom versteht, muss die Zahl 6 in das Binär System umgewandelt werden. Unser alltägliche Mathematik verwendet meistens das Dezimalsystem, sprich die Zahlen von 0 bis 9, danach kommt eine Stelle hinzu. Der Computer arbeitet, wie schon erwähnt, mit dem Binärsystem, 6 wäre dann 110. Dies packt der Computer dann in Blöcke, viele werden bestimmt schon 64 Bit gehört haben, das bedeutet das der Computer mit 64 Bit Blöcken arbeitet. Einfachhalber nehme ich ein altes System mit 8 Bit. Die 6 wäre dann mit einem 8 Bit-System 00000110, sprich der Block wird mit Nullen aufgefüllt. Wenn wir jetzt noch, wie bei der Vigenère Chiffre, ein Passwort zur Verschlüsselung ran ziehen. Kann die Zahl 6 mit z.B. einem G verschlüsselt werden. Wir haben also unsere 6 mit dem Binärcode 00000110 und unser G mit 01000111. Diese werden jetzt mit dem logischen Gatter XOR verschlüsselt. Dabei wird jede Stelle mit einem exklusiven Oder verglichen, das bedeutet, das die einzelnen Stellen unterschiedlich sein müssen, dann kommt eine 1 bei raus sonst wird es eine 0. Bei der 6 steht an erster Stelle eine 0 und bei dem G auch eine 1, deswegen ist die erste Verschlüsselte Stelle eine 1. Bei der zweiten Stelle stehen bei beiden Zeichen eine 1, deswegen ist die zweite verschlüsselte Stelle eine 0. Das machen wir jetzt für alle Stellen und bekommen den Binärcode 1 6-Nullen 1 (11000001). Damit wäre unsere 6 mit dem G codiert und verschlüsselt.

Dieses Verschlüsselungssystem hat starke Ähnlichkeiten mit der Vigenère Chiffre bloß ein wenig moderner. Es gilt aber immer noch, dass das Passwort genauso lang sein muss wie der zu verschlüsselnde Text, sonst kann man dieses System knacken.

RSA Verschlüsselung

Die RSA Verschlüsselung verwendet heutzutage jeder so gut wie täglich, wenn ihr z.B. im Browser ein Vorhängeschloss seht, bedeutet das, dass ihr verschlüsselt kommuniziert. Diese kommunikation ist standardisiert und verwendet RSA. Wenn ihr euch jetzt fragt, ich hatte doch noch nie Kontakt zu dieser Website, woher soll das Verschlüsselungspasswort kennen? Da gibt es einen Clou, RSA hat 2 Schlüsselpaare, ein öffentlichen und ein privaten. Mit dem öffentlichen Schlüssel wird die Nachricht verschlüsselt und mit dem privaten Schlüssel kann die Nachricht entschlüsselt werden. Das kann man sich so vorstellen, dass es ein Schlüssel für eure Haustür zum verriegeln und ein Schlüssel zum entriegeln gibt. Den Schlüssel zum verriegeln kann jeder Mensch auf diesem Planeten haben, komplett ungefährlich, da ja nur verschlossen werden kann. Aber nur ihr solltet den Schlüssel zum aufschließen besitzen. Wir haben jetzt gelernt, dass es 2 Schlüsselpaare gibt und der eine zum verschlüsseln und der andere zum entschlüsseln ist. Wenn ihr jetzt eine Website ansurft, sendet ihr dieser Website den öffentlichen Schlüssel, die Website schnürt dann ein Datenpaket und verschlüsselt dieses Paket mit dem öffentlichen Schlüssel und sendet euch das Paket. Theoretisch könnte euer Internetanbieter diese Pakete mitlesen, aber da dieser nicht den privaten Schlüssel besitzt, kann der Anbieter das Paket nicht öffnen. Nur ihr könnt mit eurem privaten Schlüssel das Paket öffnen.

Wie funktioniert das ganze?

Dies ist ein Mathematisches System, das mit Primzahlen arbeitet. Es werden 2 große Primzahlen multipliziert, sagen wir 13 und 37, multipliziert man diese beiden Primzahlen kommt 481 raus. Jetzt macht man das nochmal, aber diesmal werden die Primzahlen minus 1 gerechnet. 12 mal 36 ist 432. Jetzt brauchst du eine natürliche Zahl, die kein Teiler von 432 ist, sagen wir 175. Nun muss 175 Modulo 432 invertiert werden, das ergibt 79. Der öffentliche Schlüssel besteht aus 175 und 481, sprich unser Faktor aus den beiden Primzahlen und der Nichtteiler. Der private Schlüssel besteht aus 79 und aus der letzten Rechnung 481. Die Nachricht muss eine Zahl sein, genauso wie es bei der Binärverschlüsselung war. Diesmal muss es aber eine Dezimalzahl sein. Wenn der Server jetzt die Geheimzahl 13 verschlüsseln will, muss der Server 13 hoch 175 modulo 481 rechnen und schicken. Die verschlüsselte Nachricht würde 351 sein. Um die Nachricht jetzt zu entschlüsseln, muss 351 hoch 79 modulo 481 und das ergibt 13.